Newton's Method for Root Finding
Implements a class for finding the roots of a function f(x).
An important problem in maths and physics is determining the roots of a function - the points at which a function f(x) is valued at 0.
Sometimes, the roots of a function can be found analytically. Another approach is to find them using an algorithm.
The algorithm described here was developed in the 17th century by Isaac Newton and Joseph Raphson.
The following shows an example run of the method:
The user is prompted for an initial guess for the root. The algorithm then computes the root to predefined precision.
Provided the function is continuous, the method is guaranteed to eventually converge to the correct root.
This programme was written in C#.
The code for this project is available here
How the Method Works
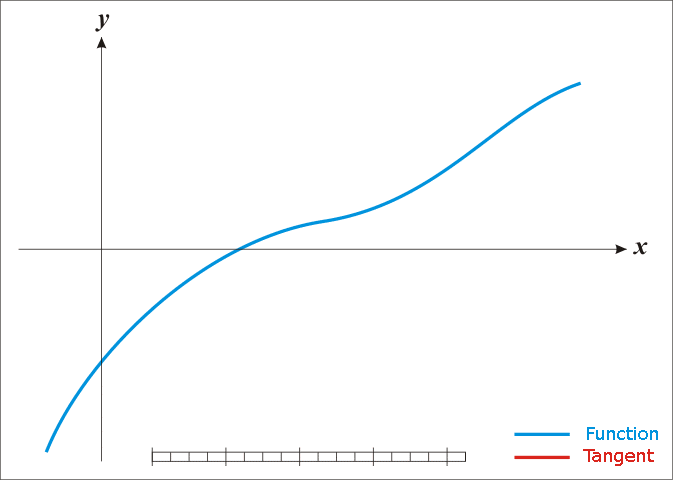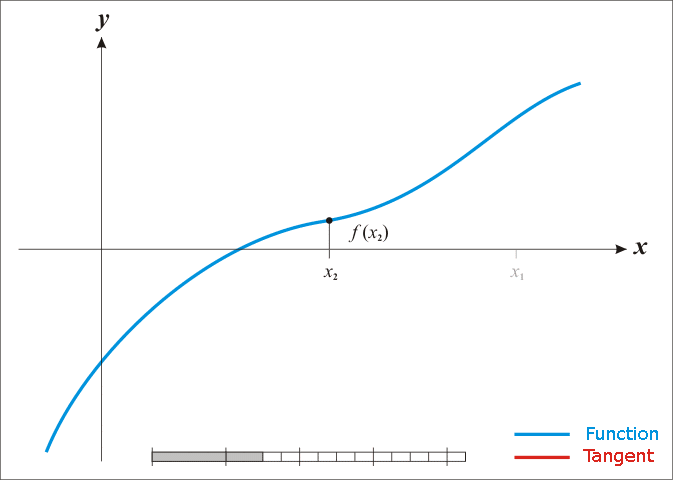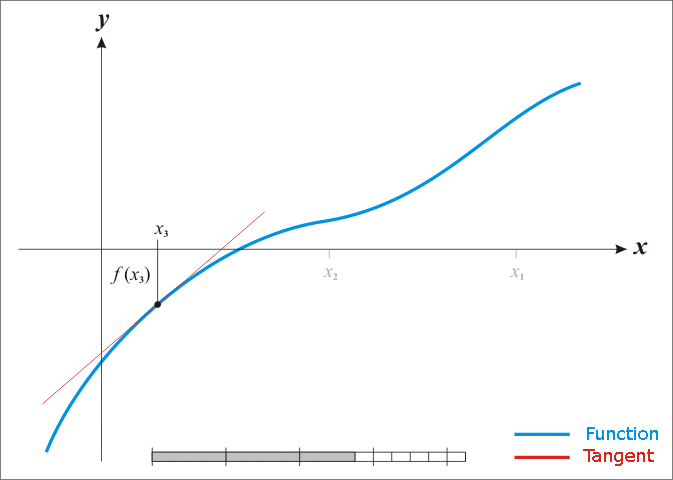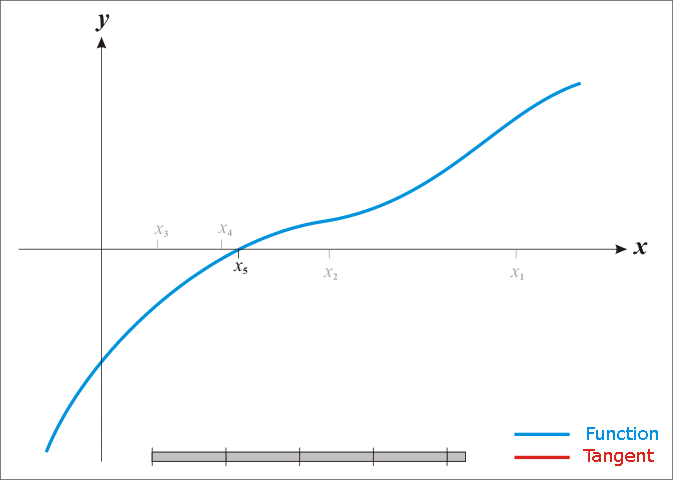
The algorithm starts with an initial guess for the root x1
The algorithm then computes the equation of the tangent to the function at the point ( x1, f(x1) )
The next guess X2 is calculated using the intersection of the tangent with the x axis.
This method can be expanded to give a general relation between two terms:
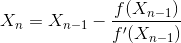
The algorithm is repeated to give greater and greater accuracy.
The algorithm stops once the difference between two subsequent guesses is less than a predefined tolerance.
By default the tolerance is 10-6.
Image Credits:
Newton Method Animation By Ralf Pfeifer - de:Image:NewtonIteration Ani.gif, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2268473